「慣性モーメントってなに?」
「回転の運動方程式を教えてほしい…!」
このような疑問を解決します。
こんにちは。機械設計エンジニアのはくです。
2019年に機械系の大学院を卒業し、現在は機械設計士として働いています。
本記事では、機械力学を学ぶ第5ステップとして「慣性モーメントと回転の運動方程式」について解説します。
この記事を読むとできるようになること。
- 慣性モーメントとは何かがわかる
- 回転の運動方程式が使いこなせるようになる
- 角運動量保存の法則がわかる
前々回の記事では質点に対する運動方程式を考えましたが、今回は回転の運動方程式を考えます。
機械力学では、並進だけでなく回転を伴う機構もたくさん扱いますので、ぜひここで理解しておきましょう。
剛体とは

回転の運動方程式を考えるときに必要なのが、「剛体」の概念です。
剛体とは、力を加えても変形しない仮想的な物体のこと。
質点と違って大きさや形を持った物体として扱えるので、「重心」や「慣性モーメント」といった物理量を考えることができます。
質量・重心・慣性モーメントの3つは、剛体の3要素と言われます。
質量とは
質量とは、その名のとおり物質の量のこと。単位はキログラム[kg]です。
機械設計では荷重という言葉もよく使いますが、こちらは質量に重力加速度gをかけたもの。
単位はニュートン[N]になります。
(荷重)=(質量)×(重力加速度)[N]
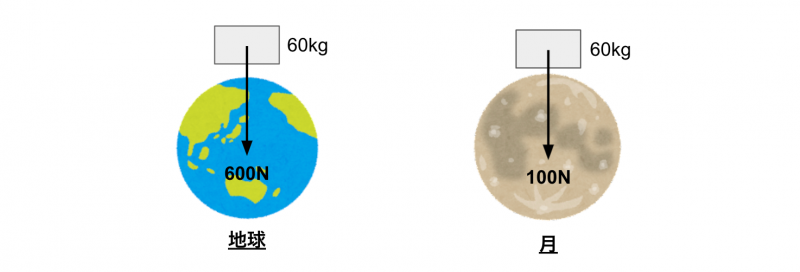
ちなみに、質量は地球にいても宇宙にいても同じ値ですが、荷重はその場所の重力加速度によってかわります。
たとえば、月は重力が地球のおよそ1/6です。
したがって、同じ質量の物体でも、発生する荷重(重力)は、地球のときの1/6になります。
重心とは
重心とは、物体の質量分布の平均位置です。
質量中心とも言われ、単位はメートル[m]を使います。
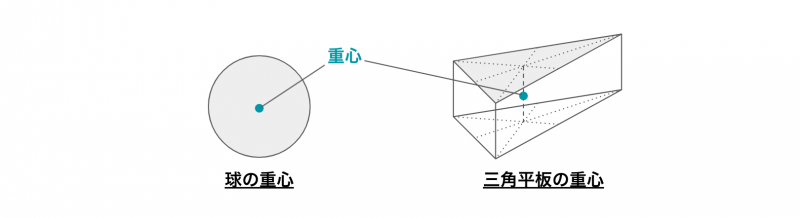
たとえば、球の重心は球の中心になりますし、三角平板の重心は各辺の中点を結んだ交点で、厚み方向は真ん中の点です(上図)。
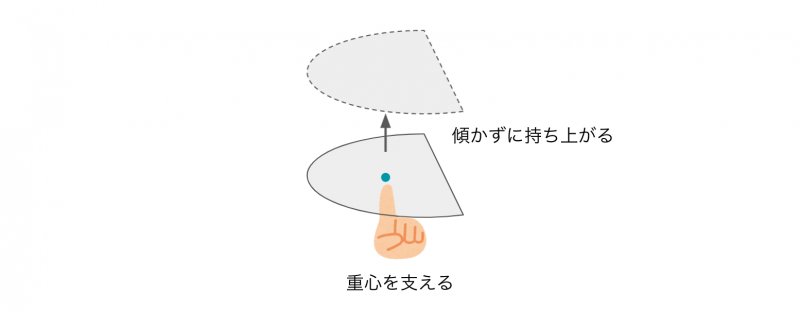
また、重心に力を加えると、物体は傾いたり回転したりすることなく移動します。
この性質は、重心が質量の平均位置であり、重心周りで考えると質量の偏りがないことを表しています。
慣性モーメントとは
慣性モーメントとは、物体の回転のしにくさを表したパラメータです。単位は[kg・m2]。
たとえば、ある軸に長さr[m]のひもで連結された質点m[kg]を考えます。
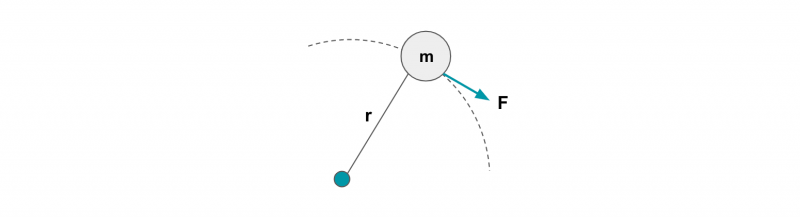
この質点に、円周方向にF[N]の推力を与えると、運動方程式は以下のとおり。
したがって、加速度は「x”(t) = F/m」です。
mx’’(t)a = F ・・・①
ここで、質点はひもで拘束されているため、軸回りに周回運動を行います。
このときのトルク(回転力)τは、以下のとおりです。
τ = F × r [N・m] ・・・②
また、回転角度をθ[rad]とすると、扇形の弧の長さから以下の関係が成り立ちます。
x(t) = rθ(t) [m] ・・・③
xを2回微分したものが加速度aなので、①〜③から以下の式が得られます。
mr2θ’’(t) = τ
I × θ’’(t) = τ
このとき、mr2が慣性モーメントI、θ’’(t)が角加速度(回転角度の加速度)です。
式から、トルクτが同じ場合、慣性モーメントIが大きくなると、角加速度が小さくなることがわかります。
つまり、慣性モーメントIは回転のしにくさを表すのです。
慣性モーメントは回転軸からの距離r[m]に依存するので、同じ物体でも回転軸が変化すると値も変わります。
物体によって1つに決まるものではなく、形状や回転の種類によって変化します。
角度と角速度と角加速度

回転運動に関係する物理量として、角速度と角加速度について簡単に説明します。
まずは角速度について。
角速度は、1秒あたりの回転角度[rad]を表したもので、単位は[rad/s]です。
機械設計の仕事では、1秒ではなく1分あたりに何回転するかを表した[rpm]という単位が用いられます。
たとえば、ポンプの回転数が120[rpm]となっていれば、1秒間に2回転(1分間に120回転)しているという意味です。
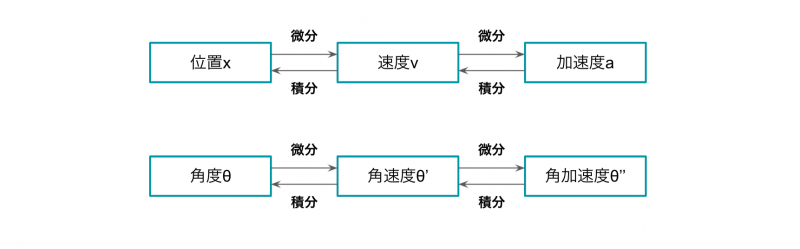
角度が時間によって変化する場合、角度θ(t)を微分すると、角速度θ’(t)が得られます。
さらに、この角速度θ’(t)を微分したものが、角加速度θ’’(t)です。
角加速度は、1秒間に角速度がどれくらい増加(減少)したかを表す数値です。
直線運動における加速度a[m/s2]に相当します。
角度、角速度、角加速度の関係を表すと、以下のようになります。
まとめ:慣性モーメントは回転のしにくさを表す

記事のポイントをまとめます。
- 力を加えても変形しない仮想的な物体が剛体
- 質量・重心・慣性モーメントが剛体の3要素
- 物体の回転のしにくさを表したパラメータが慣性モーメント
- 慣性モーメントは、同じ物体でも回転軸からの距離依存して変わる
- 1秒あたりの回転角度を表した数値が角速度
- 機械設計では、1分あたりの回転数である[rpm]が用いられる
- 角度を微分すると角速度、角速度を微分すると角加速度になる
以上です。
今回は、回転運動で重要な慣性モーメントについて説明しました。
正直、1回読んだだけではイマイチ理解できなかったという方もいると思います。
「よくわからなかった」という方は、実際に仕事で扱うようになったときに改めて読み返しみることをおすすめします!
次の記事はこちら。




コメント