「水頭ってなに?」
「エネルギーとは何が違うの?」
「どういう場合に使える?」
このような疑問を解決します。
こんにちは。機械設計エンジニアのはくです。
2019年に機械系の大学院を卒業し、現在は機械設計士として働いています。
本記事では、流体力学を学ぶ第4ステップとして「エネルギーと水頭」について解説します。
この記事を読むとできるようになること。
- 水頭とは何かがわかる
- エネルギーとの違いがわかる
- 水頭の使い方がわかる
水頭はベルヌーイの定理を応用した概念です。
ベルヌーイの定理との違いや具体的な使い方をわかりやすく解説しますので、ぜひ参考にしてください。
前回の記事はこちら
水頭とは

水頭とは、流体のエネルギーを水の高さの単位(m)で表したものです。
水頭を使うと、運動エネルギーは速度水頭V、位置エネルギーは位置水頭H、圧力エネルギーは圧力水頭Pで表されます。
また、これらの和は全水頭Eと呼ばれ、ベルヌーイの定理から以下のエネルギー保存則が成り立ちます。
E = V + H + P
ここで、ベルヌーイの定理は粘性や熱、摩擦による損失がない場合にのみ適用できるという条件がありました。
これらのエネルギー損失を損失水頭Lとして表すと、以下の保存則が成り立ちます。
E = V + H + P + L
損失水頭Lは、発生するエネルギー損失を、過去の文献や実験などからあらかじめ求めておく必要があります。
たとえば、ブラジゥスの式やニクラーゼの式は、流体の粘性や流速と損失水頭の相関関係を表した式ですから、これらを使うのもOK。
あるいは、機械設計の仕事なら、実際に実験をして損失水頭の大きさを求めておくといった感じです。
損失水頭がわかれば、さきほどのエネルギー保存の式に下記を代入して、各値を求めることができます。
| 速度水頭V | u2/2g |
| 位置水頭H | h |
| 圧力水頭P | p/ρg |
| 損失水頭L | l |
ベルヌーイの定理の応用例2つ

ここからは、ベルヌーイの定理の応用を2つ紹介します。
ベンチュリー管による流速の測定
ベンチュリー管とは、断面積が変化した管に流体を流し、2点間の圧力を測定することによって流量・流速を求める流量測定器です。
連続の式から、管の断面積が変化すると流速も変化します。
具体的に言うと、管が太いところでは流速が遅く、管が細いところでは流速が速くなります。
そこで、断面積が異なる2ヶ所の圧力を測定することで、ベルヌーイの定理から流速が求まります。
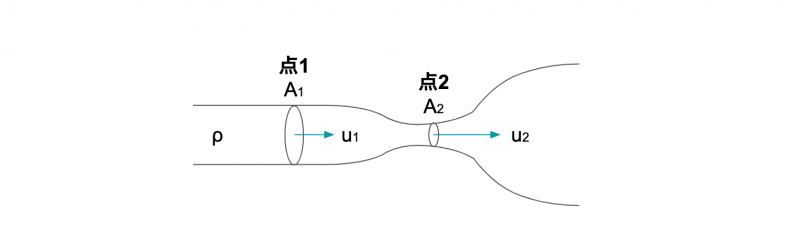
Q = u1A1 = u2A2 ・・・①連続の式
ベンチュリー管における圧力の測定方法ですが、断面積が異なる2点にU字管圧力計を取り付けて測定します。
U字管内に入れられた密度ρ’の流体は、2点の圧力差に応じて高さの差が発生するため、圧力差を測定することができます。
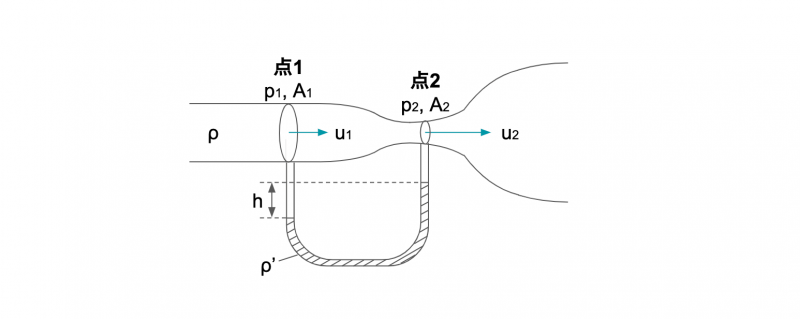
具体的な計算方法は以下のとおり。
まず、ベンチュリー管の断面積が異なる点1、2において、ベルヌーイの定理を適用します。
流れが水平なので、位置水頭はH=0です。
流速と圧力が変化するため、速度水頭Vと圧力水頭Pが変化します。
u12/2g + p1/ρg = u22/2g + p2/ρg ・・・②流管内のベルヌーイの式
つづいて、U字管内の流体にベルヌーイの定理を適用します。
流体は静止しているので速度水頭はV=0、高さの差をhとすると以下の式が成り立ちます。
p1/ρvg = h +p2/ρ’g ・・・③U字管内のベルヌーイの式
①②③から、ベンチュリー管内を流れる流体の流速と流量を求めることができます。
ちなみに、流速の測定範囲によって、U字管内に入れられる液体は異なります。
圧力差が大きくなるとU字管が長くなってしまうため、密度の大きな水銀がよく使われます。
ピトー管による流速の測定
ピトー管とは、水平管の1点に垂直にガラス管を取り付け、もう1点に流れと平行になるようにガラス管を取り付けて流速を求める計測器です。
2点間にベルヌーイの定理を適用することで、流速がわかります。
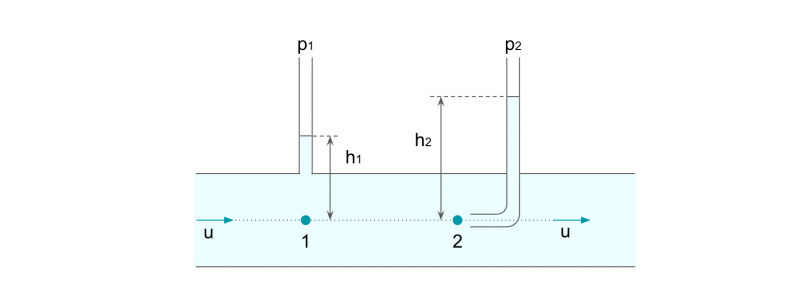
u2/2g + p1/ρg = p2/ρg
点2では、ガラス管先端で流れがせき止められます。
したがって、速度エネルギーが圧力エネルギーに変換されて、ガラス管の水位がh2まで上昇するのです。
これに対して点1では、管内の静圧p1によって、ガラス管に水が流入し水位がh1まで上昇します。
したがって、2点間の圧力差p2-p1を求めることで、管内の流速uが求まります。
p2-p1 = ρg(h2-h1)
u = √{2g(h2-h1)}
まとめ:液体のエネルギーは水頭で表せる

記事のポイントをまとめます。
- 水頭とは、流体のエネルギーを水の高さの単位(m)で表したもの
- 運動エネルギーを速度水頭V、位置エネルギーを位置水頭H、圧力エネルギーを圧力水頭P、エネルギー損失を損失水頭Lで表す
- 流体では「エネルギーの保存式:E = V + H + P + L」が成り立つ
- ベンチュリー管やピトー管は、ベルヌーイの定理を使って流量・流速を求める計測器
以上です。
水頭を使うと、ベルヌーイの定理は様々な状況に適用できます。
今回紹介した内容を応用すれば、機械設計の仕事に適した流速・流量・圧力・損失などを求めることができるでしょう。
みなさんも、ぜひベルヌーイの定理を使いこなせるようになってください!
次の記事はこちら。




コメント