「気体の状態方程式ってなんだっけ…?」
「そもそも理想気体ってなに?」
「ボイル・シャルルの法則との違いは…?」
このような疑問を解決します。
こんにちは。機械設計エンジニアのはくです。
2019年に機械系の大学院を卒業し、現在は機械設計エンジニアとして働いています。
本記事では、熱力学を学ぶ第3ステップとして、「気体の状態方程式」について解説します。
この記事を読むとできるようになること。
- 気体の状態方程式とは何か理解できる
- 気体の状態方程式を使いこなせるようになる
機械設計の仕事では、式を暗記するよりも気体の状態方程式の意味を理解して使いこなせることが大切。
授業で習ってないという方にもわかりやすく解説するので、ぜひ参考にしてください。
前回の記事はこちら。
気体の状態方程式とは

はじめに言っておくと、状態方程式は気体に適用される法則です。
液体や個体には使えないので、注意してください。
(厳密には、理想気体にしか使えないという制限がありますが、ほとんどの場合、機械設計においては無視してOK。)
0[K]まで冷やしても液体・個体にならない、理論上の仮想気体のこと。
実在気体には、分子間力があり、分子が体積を持つため、厳密には気体の状態方程式が完全には成り立たない。
そこで、分子間力がなく、分子の大きさも持たない仮想的な気体として扱うことで、状態方程式を成り立たせることができる。
質量m[kg]、温度T[K]の気体が容積V[m3]の容器に入れられているとき、圧力p[Pa]との関係は以下の式で表され、これを気体の状態方程式と呼びます。
pV = mRT
温度の単位は摂氏[℃]ではなく、絶対温度[K]なので注意してください。
「絶対温度ってなに?」という方は、前回の記事をどうぞ。
また、Rは気体定数と呼ばれる定数で、気体ごとに決まった値です。
気体定数R[J/(kg・K)]に、気体の分子量M[kg/mol]をかけた値はすべての気体で同一となります。
R = 8.31 [J/(mol・K)]
具体的な数字は、ここでは覚えなくてもOKです。
気体の状態方程式は、質量m[kg]の代わりに物質量n[mol]を使ったり、容積V[m3]の代わりに比容積(1kgあたりの容積)v[m3/kg]を使ったりと、状況によって式が変わります。
しかしながら、これらの式はネットで検索すれば出てくるので、ムリして暗記しなくてもOK。
機械設計においては、式自体を覚えることよりも、状態方程式の意味を理解して使えるようにしておくことが大切です。
気体の状態方程式が表す意味とは

では、さきほど紹介した気体の状態方程式の意味について、具体例を使って説明していきます。
状態方程式で重要なのは、圧力p[Pa]・容積V[m3]・温度T[K]の3つ。
これらは気体の状態によって、値が変化するからです。
したがって、この3つの値に注目することで、状態方程式の意味がわかるようになります。
等温変化(ボイルの法則)
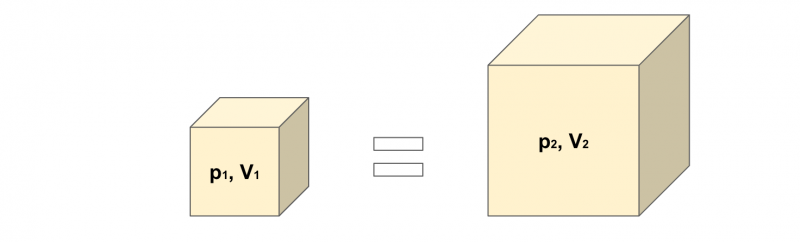
気体の状態方程式から、温度T[K]が一定の場合、気体の容積V[m3]は圧力p[Pa]に反比例することがわかります。
これをボイルの法則と言います。
pV =(一定)
図で描くと以下のようなイメージ。
p1V1 = p2V2 =(一定)
定圧変化(シャルルの法則)
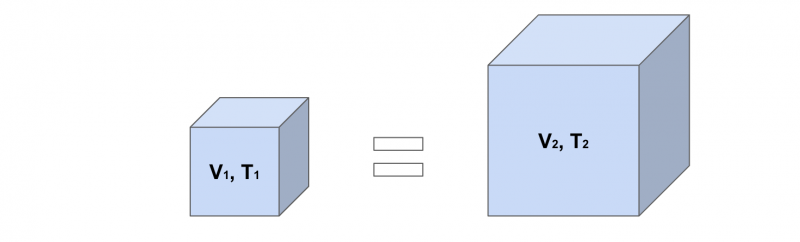
つづいて、圧力p[Pa]が一定の場合、気体の容積V[m3]は温度T[K]に比例します。
これをシャルルの法則と言います。
V1/T1 = V2/T2 =(一定)
定容変化
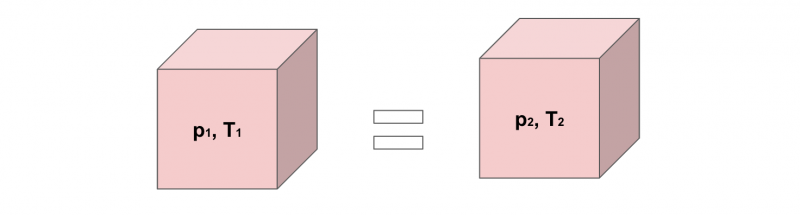
さいごに、気体の容積V[m3]を一定にすると、圧力p[Pa]は温度T[K]に比例します。
p1/T1 = p2/T2 =(一定)
以上、3つの変化に注目して、状態方程式の意味を説明しました。
実際の仕事では、これらを組み合わせながら設計に応用していくことになります。
たとえば、「一定の容積内に入った気体の温度を下げるにはどうすればいいかな」→「定容変化では温度と圧力が比例するから、圧力を下げればいい」といった感じ。
製品の使用条件や環境に応じて様々な要因が影響するので、状態方程式を使いこなすには知識と経験が必要です。
まとめ:気体の状態方程式を使いこなそう

記事のポイントをまとめます。
- 状態方程式は気体にのみ適用できる
- 温度の単位は[K](ケルビン)
- 温度T[K]が一定の場合、気体の容積V[m3]は圧力p[Pa]に反比例する
- 圧力p[Pa]が一定の場合、気体の容積V[m3]は温度T[K]に比例する
- 気体の容積V[m3]を一定にすると、圧力p[Pa]は温度T[K]に比例する
以上です。
高校や大学では、気体の状態方程式を使って問題が解けることが大切でしたが、機械設計においては、状態方程式の意味を理解して使えることが大切です。
一度で理解できなかったという方は、繰り返し記事を読んでみて、使いこなせるようになってください!
次の記事はこちら。




コメント