「せん断力図と曲げモーメント図の書き方がわからない…」
「そもそも、せん断力と曲げモーメントってなんだっけ?」
このような疑問を解決します。
こんにちは。機械設計エンジニアのはくです。
2019年に機械系の大学院を卒業し、現在は機械設計士として働いています。
本記事では、材料力学を学ぶ第7ステップとして「せん断力図と曲げモーメント図の書き方」を解説します。
この記事を読むとできるようになること。
- せん断力とは何かがわかる
- 曲げモーメントとは何かがわかる
- せん断力図と曲げモーメント図の書き方がわかる
せん断力図と曲げモーメント図の書き方は、材料力学の授業や試験でよく出てきます。
大学の授業だけじゃわからなかったという方は、ぜひこの記事を読んで理解しておきましょう。
前回の記事はこちら。
せん断力とは
せん断力とは、下図の向きに作用する力のことです。
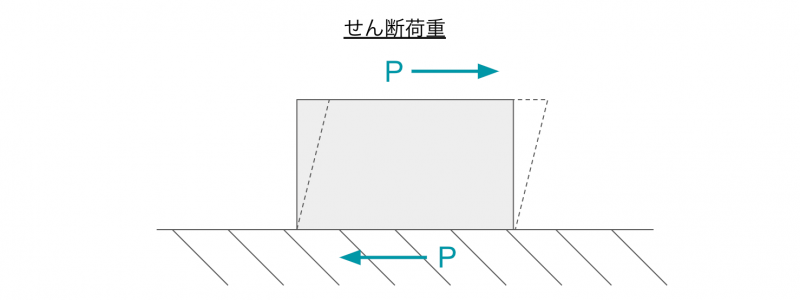
引張荷重や圧縮荷重は、2つの力が同一直線上に作用しますが、せん断荷重は力の軸がズレて作用します。
たとえば、地面に置かれた物体を引きずると、地面との摩擦によってせん断荷重が作用します。
曲げモーメントとは
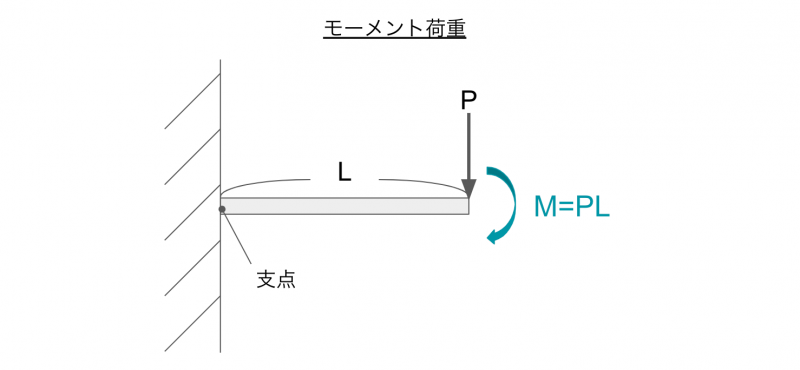
モーメントは「物体を回転させる力の大きさ」であり、(力)×(支点からの距離)で計算されます。
モーメントには、ねじりモーメントや慣性モーメントなどの種類があり、曲げモーメントもその1つ。
曲げモーメントは、部材を曲げようとする力の大きさです。
せん断力図と曲げモーメント図の書き方

ここからは、せん断力図と曲げモーメント図の書き方を、8つの例を使って具体的に解説します。
ちなみに、せん断力図はSFD(Shearing Force Diagram)、曲げモーメント図はBMD(Bending Moment Diagram)とも呼ばれます。
①集中荷重によって発生するせん断力
梁に集中荷重が作用すると、せん断力が発生します。
下図のように、片持はりに下向きの荷重Pが作用すると、支点Aには上向きの反力RAが発生します。
力のつり合いから、荷重Pと反力RAの間には以下の関係が成り立ちます。
P = RA
ここで、点Aを原点として図の向きにx軸を取ります。
力がつりあうために、AB間では梁の内部にせん断力Fxが下向きに作用します。
ただし、点Bでは荷重Pが作用しているため、せん断力FBは0です。
これをグラフ化すると、片持はりに集中荷重が作用する場合のせん断力図(SFD)が書けます。
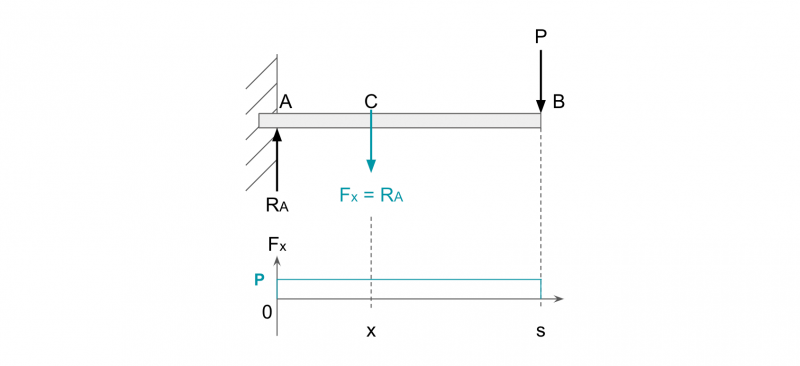
せん断力図から、Fxの大きさは支点からの距離xに関係なく一定であることがわかります。
ただし、ここでは下向きのせん断力を正の値として表しています。
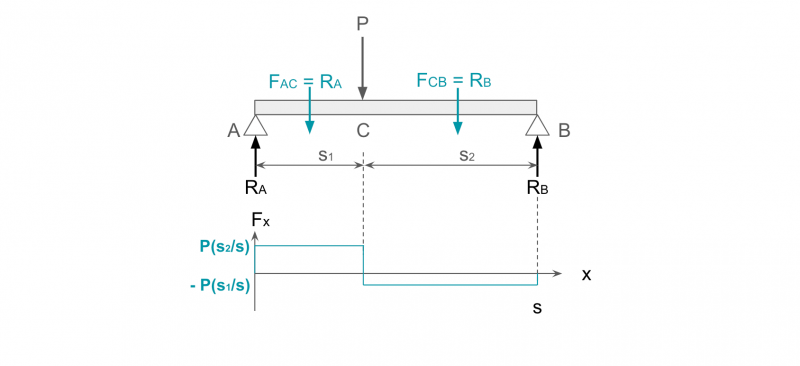
同様にして、下図のような両端支持はりに集中荷重Pが作用する場合のせん断力図を求めてみます。
支点Aから距離s1の点Cに荷重Pが作用する場合、支点A、Bにはそれぞれ反力RA、RBが発生します。
ここで、点A、Bにおけるモーメントのつり合いから、以下の式が成り立ちます。
点Aにおけるモーメントのつり合い:RB × s = P × s1
点Bにおけるモーメントのつり合い:RA × s = P × s2
これを解くと、反力RA、RBがそれぞれ求まります。
RA = P(s2/s), RB = P(s1/s)
AC間では反力RAが上向きに作用していることから、梁の内部にはせん断力FAC = RAが作用します。
同様に、CB間では反力RAが上向きに、荷重Pが下向きに作用していることから、梁の内部にはせん断力FCB = RA – P = RBが作用します。
これをグラフ化すると、両端支持はりに集中荷重が作用する場合のせん断力図は、以下のとおりです。
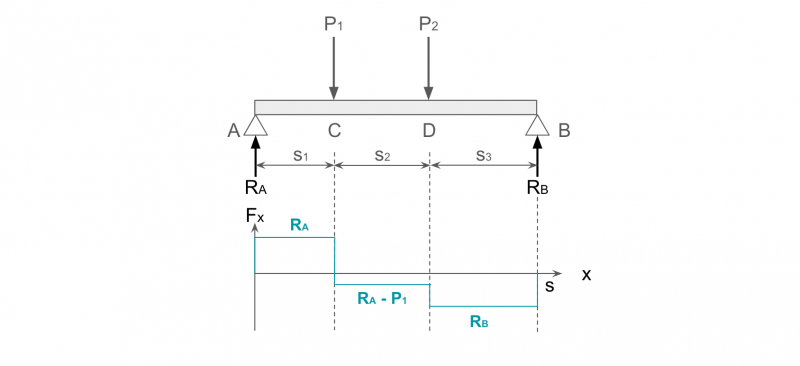
②複数の集中荷重によって発生するせん断力
集中荷重が複数発生する場合も、同様にしてせん断力を求めることができます。
下図のように、点C、Dにそれぞれ大きさP1、P2の荷重が作用している長さsの両端支持はりを考えます。
点A、Bに発生する反力をRA、RBとすると、力のつり合いから以下の式が成り立ちます。
P1 + P2 = RA + RB
ここで下向きを正の値とすると、AC間には上向きの反力RAとつり合うためのせん断力FAC = RAが、CD間には反力RAおよび荷重P1とつり合うためのせん断力FCB = RA – P1が作用します。
また、DB間には反力RA、荷重P1、P2とつり合うためのせん断力FDB = RA – (P1 + P2) = -RBが作用します。
以上より、各点におけるモーメントのつり合いから反力RA、RBを求めれば、それぞれの区間におけるせん断力Fxが求まりせん断力図が書けます。
③分布荷重によって発生するせん断力
分布荷重が発生する場合は、集中荷重と違い位置によってせん断力の大きさが変わります。
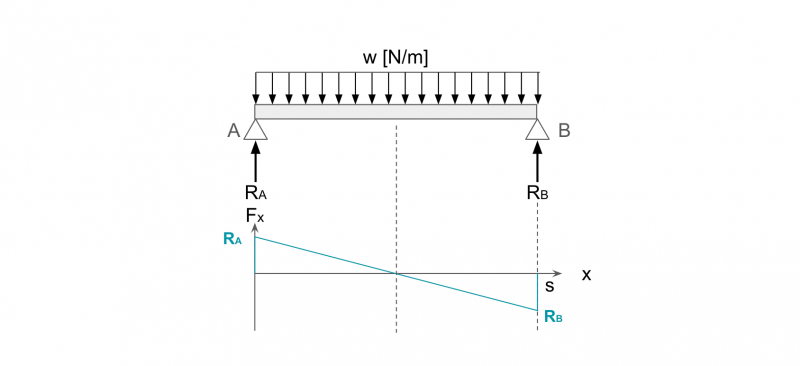
下図のように、両端支持はりの全面に等分布荷重w[N/m]が作用する場合を考えます。
w[N/m]は単位長さあたりの荷重です。
等分布荷重の場合、全荷重ws[N]は、Aに発生する反力RAと、Bに発生する反力RBによって均等に支えられるため、以下の式が成り立ちます。
RA = RB = ws/2
位置xにおける荷重はwx[N]であることから、せん断力Fxは以下の式で表されます。
Fx = RA – wx
これをグラフ化すると、分布荷重が作用する場合のせん断力図が書けます。
グラフより、梁の中心では反力RAと荷重ws/2がつり合って、せん断力が0になることがわかります。
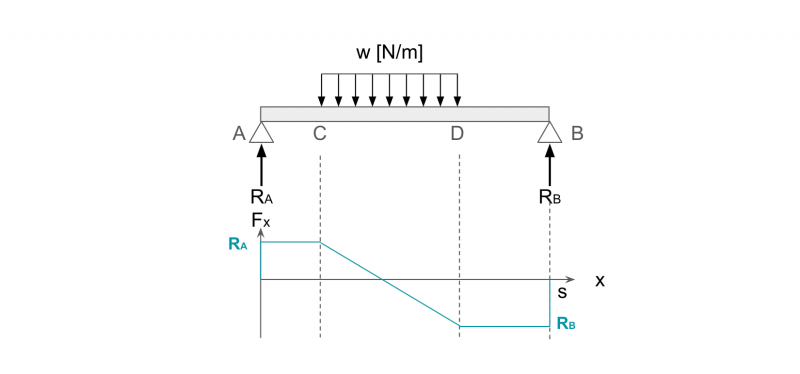
ちなみに、上記は梁全体に等分布荷重が作用する場合ですが、梁の一部に分布荷重が作用する場合も同様にしてせん断力図を書くことができます。
④片持梁に作用する曲げモーメント
つづいて、曲げモーメント図の書き方を説明します。
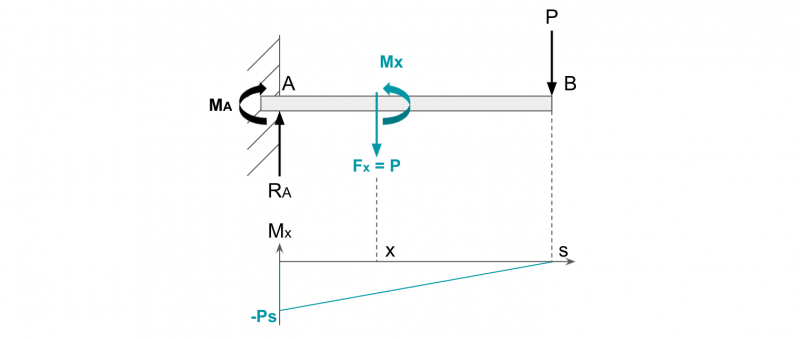
下図のように片持はりの自由端Bに、集中荷重Pが作用する場合を考えます。
固定端Aにおける曲げモーメントをMAとすると、モーメントのつり合いは以下のとおり。
ただし、曲げモーメントは梁が下に凸に変形する場合を正の値として考えます。
MA = -Ps
また①で考えたように、片持ち梁の内部には位置xに関係なく一定のせん断力が発生します(ここではFx = P)。
したがって、位置xにおける曲げモーメントをMxとすると、モーメントのつり合いは以下のとおり。
MA = -Fx・x + Mx
Mx = -P(s – x)
これをグラフ化すると、片持はりに集中荷重が作用した場合の曲げモーメント図が書けます。
上記は1箇所に集中荷重が作用する場合ですが、複数の集中荷重が作用する場合も考え方は同様です。
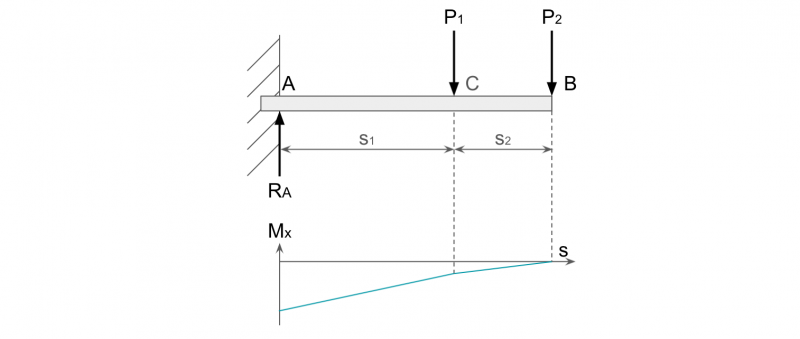
⑤両端支持梁に集中荷重が作用する曲げモーメント
両端支持はりに集中荷重が作用する場合を考えます。
荷重Pと反力RA、RBによる力のつり合い、およびモーメントのつり合いから以下の式が成り立ちます。
力のつり合い:P = RA + RB
点Aにおけるモーメントのつり合い:RB × s = P × s1
点Bにおけるモーメントのつり合い:RA × s = P × s2
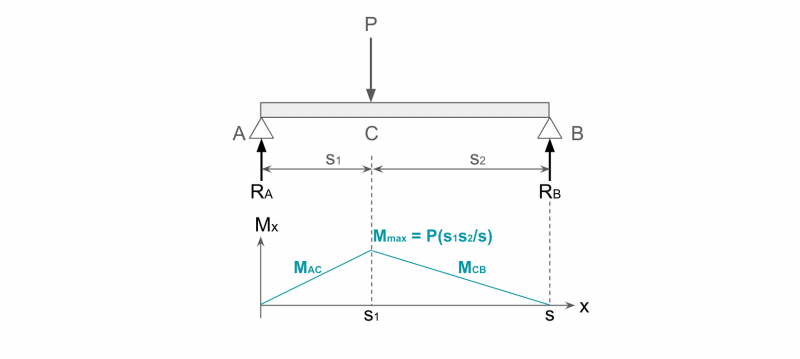
以上より、梁に作用する曲げモーメントを求めます。
AC間では、反力RAのみによる曲げモーメントが発生し、CB間では反力RAおよび荷重Pによる曲げモーメントが発生します。
それぞれをMAC、MCBとすると、梁に作用する曲げモーメントは、以下のとおり。
MAC = RAx
MCB = RAx – P(x-s1)
つり合いの式から求めたRAを代入すると、位置xにおける曲げモーメントMxが求まります。
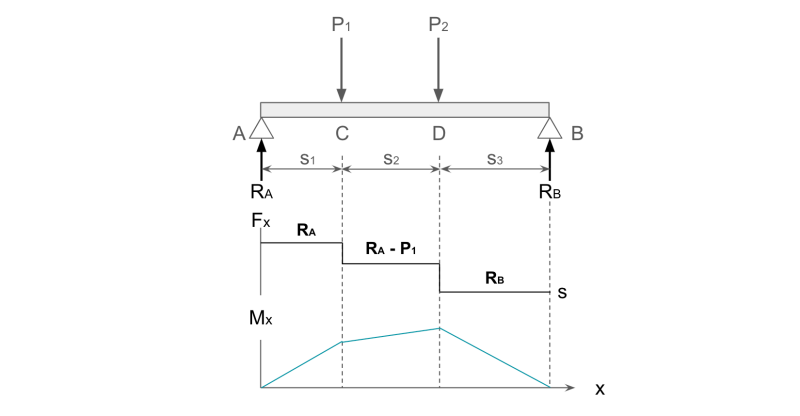
⑥複数の集中荷重が作用する曲げモーメント
両端支持はりに複数の集中荷重が作用する場合も、1つの集中荷重が作用するときと同様にして曲げモーメントが求まります。
下図のように、両端支持はりの点C、Dにそれぞれ荷重P1、P2が作用する場合を考えます。
力のつり合い、およびモーメントのつり合いから、以下の2式が成り立ちます。
RA + RB = P1 + P2
P1 × s1 + P2 × (s1 + s2) = RB × s
上記から、点A、Bにおける反力RA、RBが求まります。
ここで、点Aからの距離をxとすると、AC間の曲げモーメントMAC、CD間の曲げモーメントMCD、DB間の曲げモーメントMDBはそれぞれ以下となります。
MAC = RAx
MCD = RAx – P1(x-s1)
MDB = RAx – P1(x-s1) – P2(x-s1-s2)
この3つに、さきほど求めたRAを代入すると、距離xにおける曲げモーメントMxが求まります。
ここでは2つの荷重が作用する場合を説明しましたが、荷重が3つ、4つ…と増えていっても同じです。
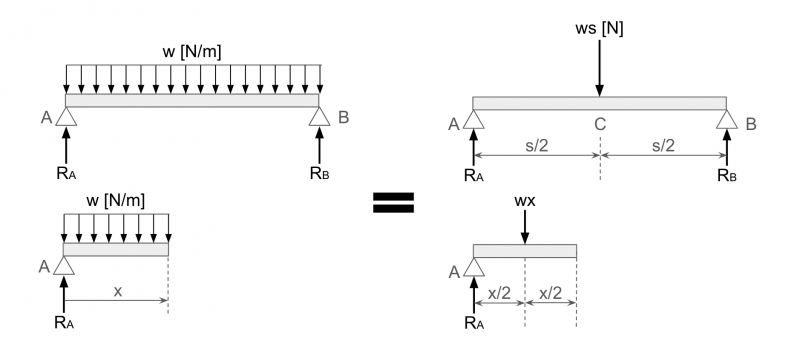
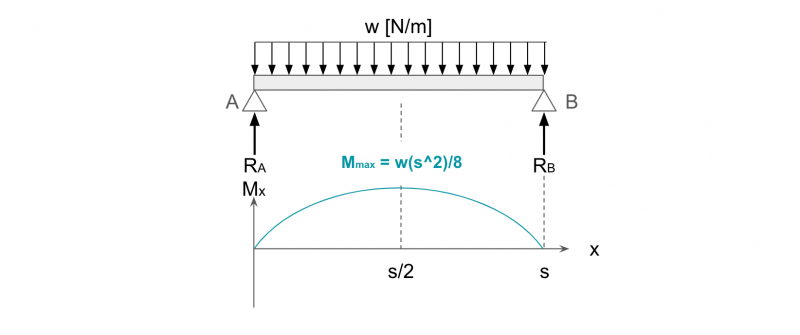
⑦等分布荷重が作用する曲げモーメント
つづいて、さきほどの両端支持はりに、等分布荷重が作用する場合の曲げモーメントを求めます。
等分布荷重が作用する梁では、分布荷重を集中荷重に置き換えて考えます。
具体的に説明すると、次のとおり。
下図のように長さsの両端支持はり全体に、等分布荷重w[N/m]が作用する場合を考えます。
せん断力の求め方で説明したように、梁全体にはws[N]の荷重がかかり、力のつり合いから反力RA、およびRBが求まります。
RA = RB = ws/2
これは、梁の中心Cに集中荷重 P=sw/2 が作用しているものと考えることができます。
同じようにして、点Aから距離xの部分に作用する曲げモーメントは、距離x/2の位置に集中荷重wx[N]が作用していると考えることで求められます。
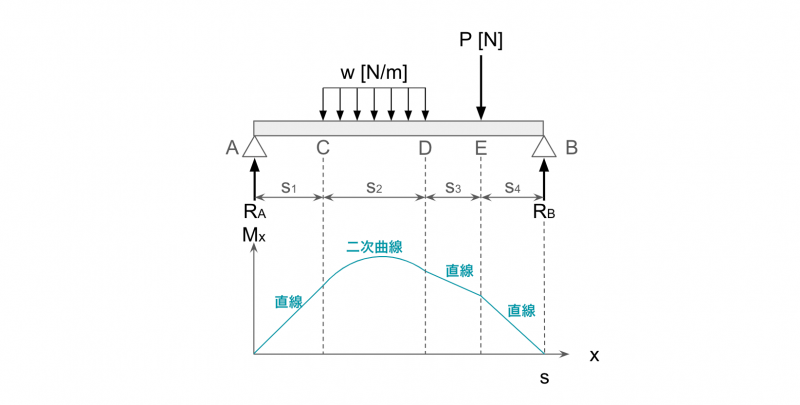
⑧集中荷重と等分布荷重が作用する曲げモーメント
さいごに、やや発展的な内容として、集中荷重と分布荷重が同時に作用する場合の曲げモーメントを説明します。
といっても考え方は同じで、力のつり合いとモーメントのつり合いから反力を求め、代入するだけです。
また、さきほど説明したように、分布荷重は集中荷重に置き換えて考えます。
力のつり合いから、
P + ws = RA + RB
支点Aにおけるモーメントのつり合いから、
RB × s = ws × s1 + P(s1 + s2/2 + s3)
したがって、各区間における曲げモーメントは次のとおり。
MAC = RAx
MCD = RAx – ws(x-s1)(x-s1)/2
MDE = RAx – ws(x-s1-s2/2)
MEB = RAx – ws(x-s1-s2/2) – P{x-ws(x-s1-s2-s3)}
以上より、曲げモーメント図が書けます。
まとめ:力とモーメントのつり合いから、せん断力図と曲げモーメント図が書ける

以上、8つの例を使ってせん断力図と曲げモーメント図の書き方を説明してきました。
せん断力図と曲げモーメント図は、材料力学の授業や試験でよく出てくる内容です。
「1回じゃイマイチよく理解できなかった…」という方は、ぜひ本記事を繰り返し読んで、せん断力図と曲げモーメント図を書けるようにしてください!
次の記事はこちら。





コメント
記事作成ありがとうございます。
④片持梁に作用する曲げモーメントまで勉強させてもらいましたが、
ここの最初のBMD で、壁のつけ根で0になっていて、変な気がします。
ご確認ください。
TAMURAさん、コメントありがとうございます。
ご指摘いただいたとおり、④の式とグラフが誤っていたので修正しました。
混乱させてしまいすみません。