たわみの公式と求め方【図解でわかりやすく解説】

「たわみの求め方が知りたい」

「断面二次モーメントってなんだっけ…？」

このような疑問を解決します。

こんにちは。機械設計エンジニアのはくです。

2019年に機械系の大学院を卒業し、現在は機械設計士として働いています。

本記事では、材料力学を学ぶ第8ステップとして「たわみの公式と求め方」を解説します。

この記事を読むとできるようになること。

たわみとは何かがわかる
たわみの公式と求め方がわかる
断面二次モーメントや断面係数についてわかる

壊れない製品を設計するためには、たわみや許容応力の計算が不可欠です。

「たわみの求め方がわからない…！」という方は、ぜひ本記事を読んで内容を理解しておきましょう。

前回の記事はこちら。

たわみとは
たわみの求め方と断面二次モーメント
1. 断面二次モーメントとは
たわみの公式と求め方
まとめ：よく使うたわみの公式は暗記しておくと便利
1. 関連

たわみとは

下図のように、両端支持はりに荷重Pが作用すると、はりは下向きに凹形に変形します。

水平方向にx軸、垂直方向にy軸を取ると、はりは-y方向に変形していることになります。

この変形量yがたわみです。

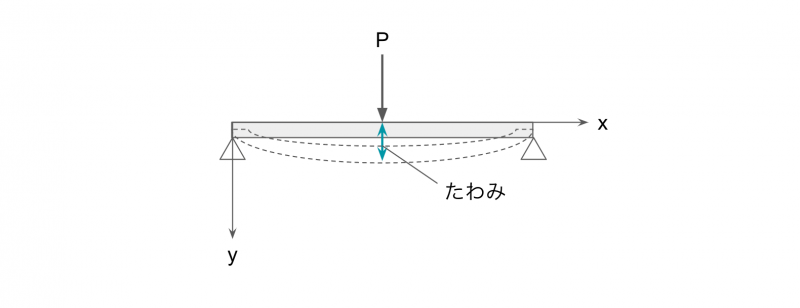
荷重がかかると部材にはたわみが発生し、製品の強度に影響を及ぼします。

たわみが大きくなると部材が破損する恐れがありますし、他の部材と干渉して強度が低下する可能性があるからです。

したがって、機械設計では、たわみを求めることが信頼性の高い製品をつくるために重要になってきます。

たわみの求め方と断面二次モーメント

梁に発生するたわみyの大きさは、曲げモーメントM(x)を2回積分することで求められます。

ただし、Eはヤング率、Iは断面二次モーメントです。

d²y/dx² = -M(x)/EI

ここで、下図のような両端支持はりの場合、支点A、Bにおけるたわみは0です。

したがって、上式を積分し、支点A、Bにおけるたわみ0の境界条件を与えることで、梁に発生するたわみを求めることができます。

ちなみに、荷重Pの作用点では、たわみが最大になります。

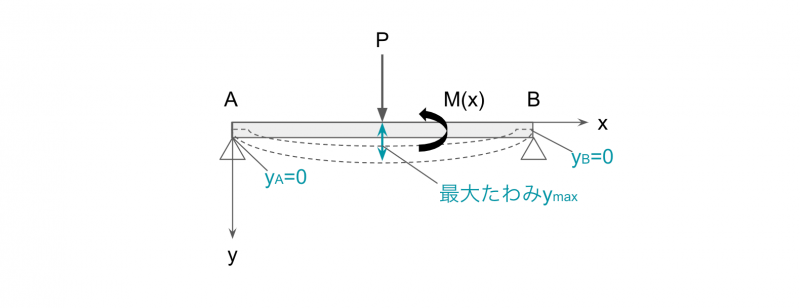
梁に発生する曲げモーメントの求め方は、前回の記事で解説しています。

せん断力図と曲げモーメント図の書き方【8つの例でわかりやすく解説】

せん断力図と曲げモーメント図の書き方を知りたいですか？本記事では、せん断力・曲げモーメントとは何かから、せん断力図と曲げモーメント図の書き方までをわかりやすく解説します。「せん断力図と曲げモーメント図の書き方がわからない…！」という方は、ぜひ記事の内容を参考にしてください。

断面二次モーメントとは

梁の断面形状によって決められる定数のこと。

代表的な断面形状と断面二次モーメントは、次のとおりです。

円の断面二次モーメント

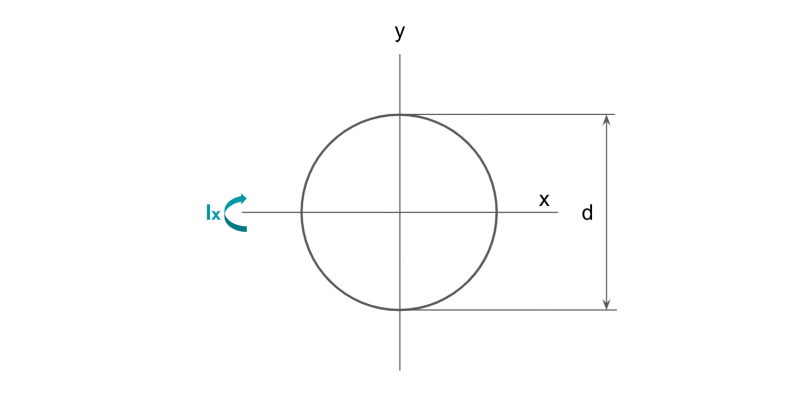
πd⁴/64

楕円の断面二次モーメント

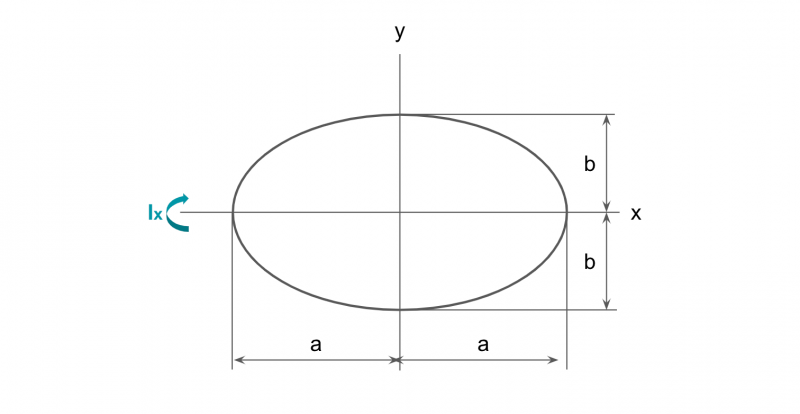
πab³/4

三角形の断面二次モーメント

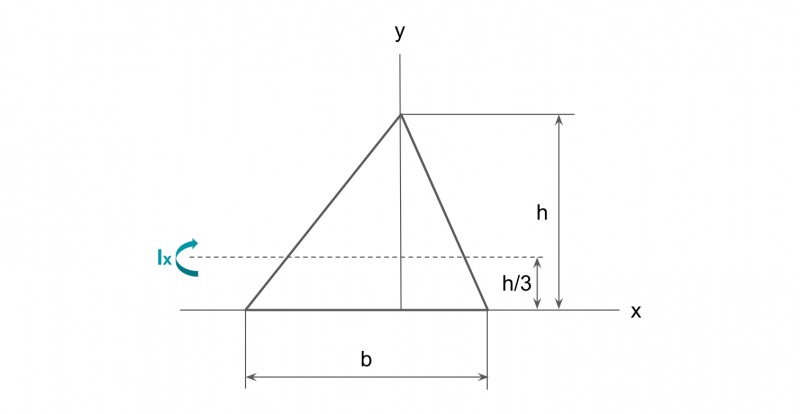
bh³/36

平行四辺形の断面二次モーメント

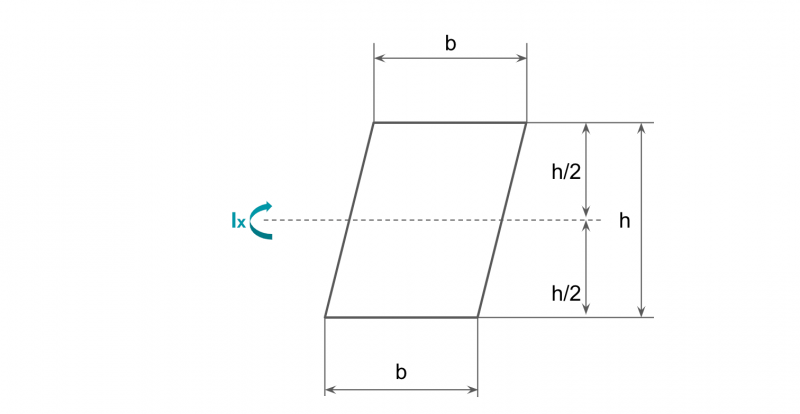
bh³/12

たわみの公式と求め方

ここからは一般的な梁のたわみとして、6つの例を紹介します。

具体的な求め方はさきほど説明したとおり。

大学の授業や試験では、公式の導出も大切ですが、実際の設計業務では以下で紹介する公式を丸暗記しておくと便利です。

片持はりに集中荷重が作用する場合のたわみの公式

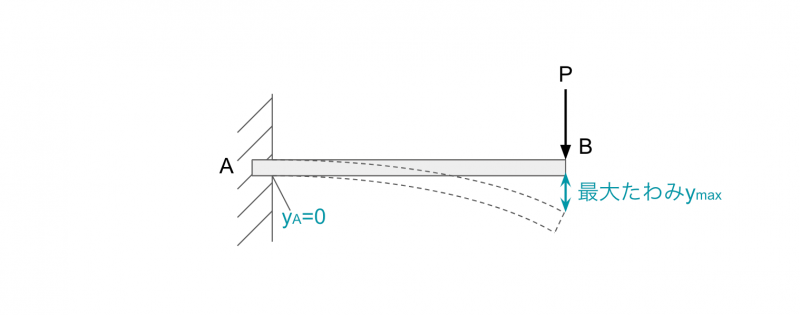
長さsの片持はりの自由端に、集中荷重Pが作用する場合のたわみの公式は、以下のとおり。

固定端Aでたわみは0、自由端Bでたわみは最大となります。

y(x) = P(x³ – 3xs²x + 2s³)/6EI

y_max = Ps³/3EI

片持はりに等分布荷重が作用する場合のたわみの公式

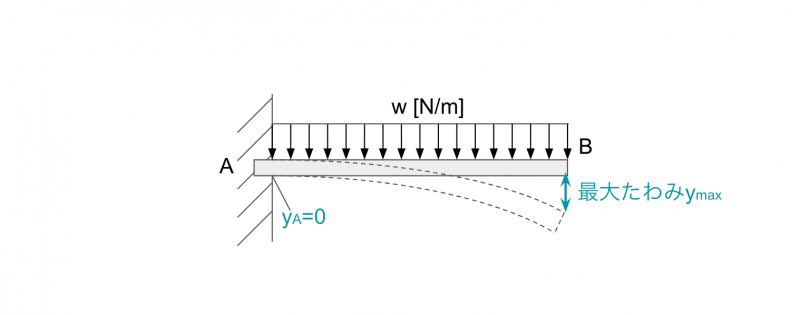
長さsの片持はり全体に、等分布荷重w[N/m]が作用する場合のたわみの公式は、以下のとおり。

さきほど同様、固定端Aでたわみは0、自由端Bでたわみは最大となります。

y(x) = w(x⁴ – 4xs³x + 3s⁴)/24EI

y_max = ws⁴/8EI

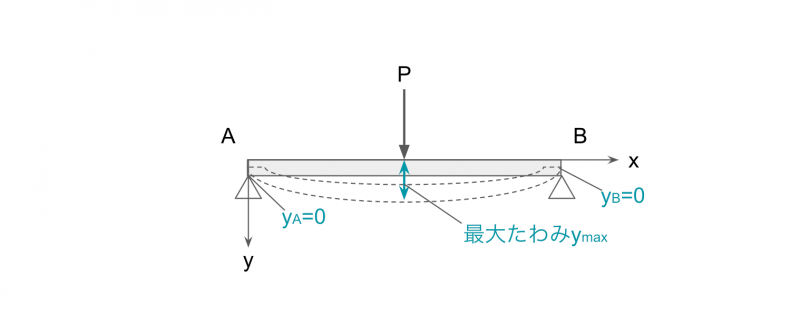
両端支持はりに集中荷重が作用する場合のたわみの公式

長さsの両端支持はりの中心に、集中荷重Pが作用する場合のたわみの公式は、以下のとおり。

支点A、Bでたわみは0、荷重の作用点Cでたわみは最大となります。

y_max = Ps³/48EI

両端支持はりに等分布荷重が作用する場合のたわみの公式

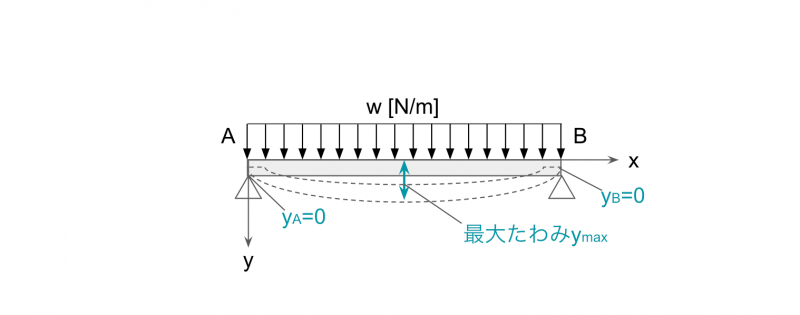
長さsの両端支持はり全体に、等分布荷重w[N/m]が作用する場合のたわみの公式は、以下のとおり。

支点A、Bでたわみは0、梁の中心Cでたわみは最大となります。

y_max = 5ws⁴/384EI

両端固定はりに集中荷重が作用する場合のたわみの公式

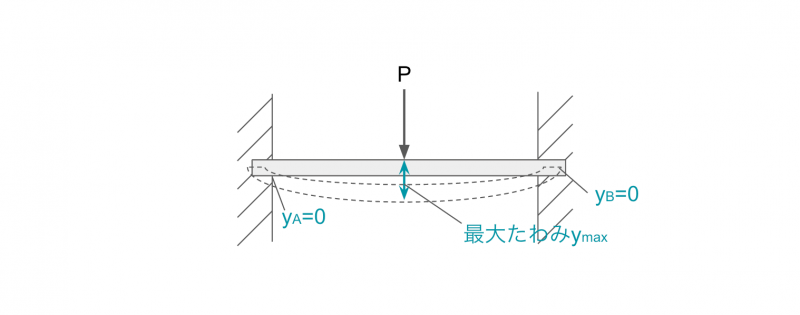
長さsの両端固定はりの中心に、集中荷重Pが作用する場合のたわみの公式は、以下のとおり。

支点A、Bでたわみは0、荷重の作用点Cでたわみは最大となります。

y_max = Ps³/192EI

両端固定はりに等分布荷重が作用する場合のたわみの公式

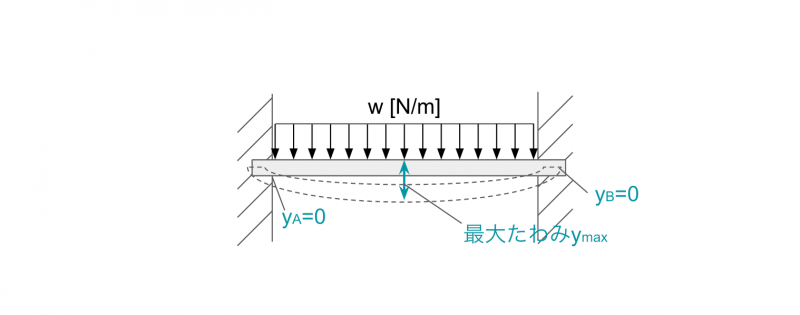
長さsの両端固定はり全体に、等分布荷重w[N/m]が作用する場合のたわみの公式は、以下のとおり。

支点A、Bでたわみは0、梁の中心Cでたわみは最大となります。

y_max = ws⁴/384EI

まとめ：よく使うたわみの公式は暗記しておくと便利

以上、たわみの公式と求め方を解説しました。

大学の授業や試験ではたわみの公式を導出できることが大切ですが、実際の設計業務ではあまり必要ありません。

機械設計をやるうえでは、よく使うたわみの公式は丸暗記しておくと便利。

強度計算やシミュレーションをするうえでも役に立つので、ぜひこの機会に覚えて使ってみてください。

次の記事はこちら。