「梁ってなんだっけ?」
「単純支持と固定支持ってなに?」
「梁に働く荷重と反力の求め方が知りたい…!」
このような疑問を解決します。
こんにちは。機械設計エンジニアのはくです。
2019年に機械系の大学院を卒業し、現在は機械設計士として働いています。
本記事では、材料力学を学ぶ第6ステップとして「梁にはたらく荷重と反力の求め方」を解説します。
この記事を読むとできるようになること。
- 梁とは何かがわかる
- 梁にはたらく荷重と反力の求め方がわかる
- 単純支持と固定支持の違いがわかる
- 集中荷重と分布荷重の違いがわかる
梁にはたらく荷重と反力を求められることは、材料力学の基本です。
機械設計の仕事ではもちろん、授業や試験の問題としてもよく出てくる内容ですので、確実に理解しておきましょう。
前回の記事はこちら。
梁とは
梁とは、構造物において荷重を受け持つ部位のことです。
下図のように水平方向にわたる部材を梁、垂直方向に立つ部材を柱と言います。
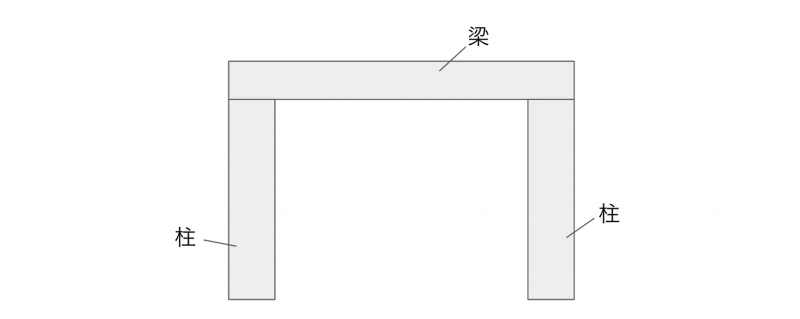
梁や柱の役割は、荷重の受け持ちと分散化です。
たとえば、家屋や高層ビルでは、異なる大きさの梁や柱を無数に組み合わされることで、荷重を分散化して支えています。
梁は、人間で言うと骨にあたる部位。
僕たち人間の骨には、脳や内臓などを保護するとともに、荷重を分散して体を支える役割があります。
梁も同じで、荷重を受け持ち、分散化させることで構造物全体を支える重要な役割を担っています。
梁の種類

梁は、支点と荷重の組み合わせによって種類がわかれます。
単純支持と固定支持
支点の種類は、固定方法によって2つ。
梁を支点の上にのせただけの単純支持(下図(a))と、壁に埋め込んで固定した固定支持(下図(b))です。
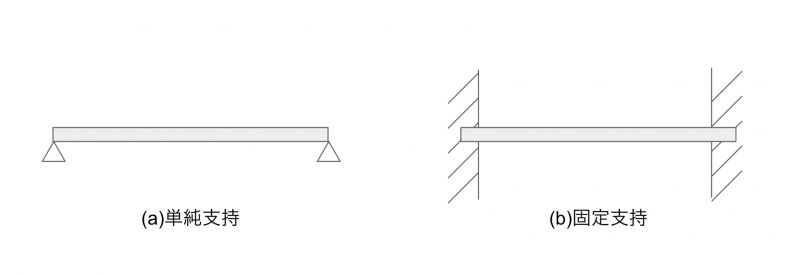
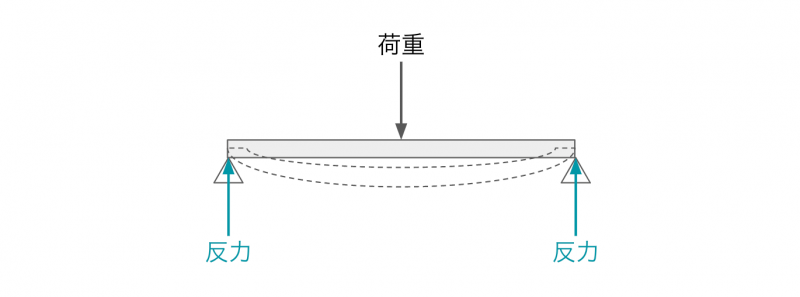
単純支持では、梁の垂直方向の変位が、支点で固定されています。
回転方向は固定されないので、梁に荷重がかかると、支点にはせん断力が作用しますが、曲げモーメントは作用しません。
梁に作用する荷重と同じ大きさで逆向きの反力が支点に作用し、力の平衡が保たれています。
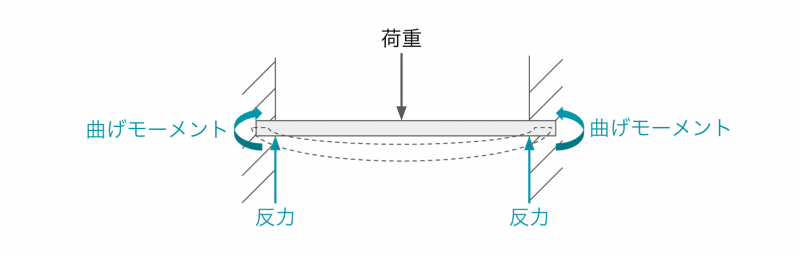
一方、固定支持では、垂直・水平・回転方向すべてが固定されます。
したがって、梁に荷重がかかると、せん断力と曲げモーメントの両方が支点に作用します。
集中荷重と分布荷重
荷重も、作用の仕方によって2種類に分けられます。
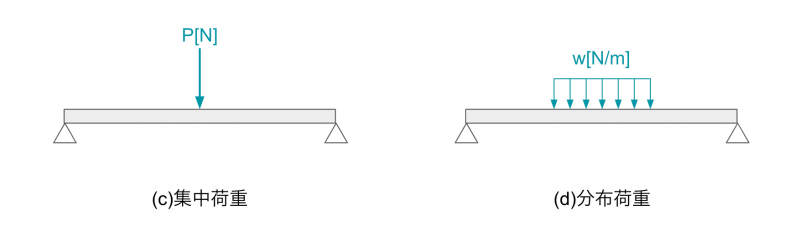
下図(c)のように点で作用する荷重を集中荷重、(d)のように面で作用する荷重を分布荷重と言います。
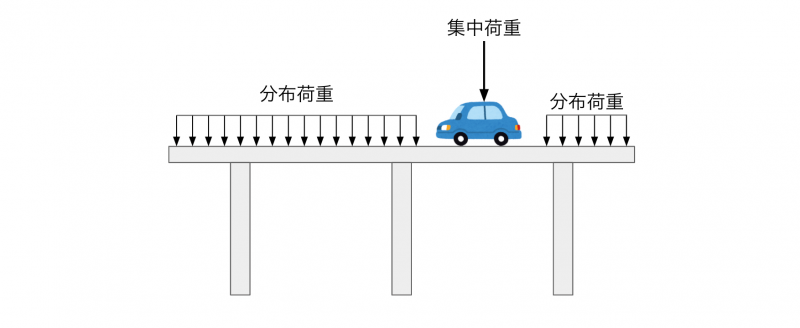
たとえば、橋の上にのっている自動車を、柱で支えるとします。
ここで、橋の自重を無視すると、柱には集中荷重として自動車の重さ分の荷重がかかることになります。
一方、橋の自重が無視できない場合、柱には自動車に加えて橋の自重分の荷重がかかります。
橋の重さは1点に集中してかかるのではなく、橋全体にまんべんなくかかるため、分布荷重がはたらくことになります。
さらに、自動車が動く場合は、時間とともに荷重が作用する場所が変わります。
それにともなって、支点に作用するせん断力や曲げモーメントの大きさも変わるため、より複雑な計算が必要になります。
梁に作用する荷重と反力の求め方

梁の種類がわかったところで、具体的に梁に作用する荷重と反力の求め方を解説します。
集中荷重による反力の求め方
下図のように、長さsの両端支持はりにおいて、点Cに荷重Pが作用する場合を考えます。
このとき、両端の支点A、Bには、荷重Pと逆向きの反力RA、RBが作用します。
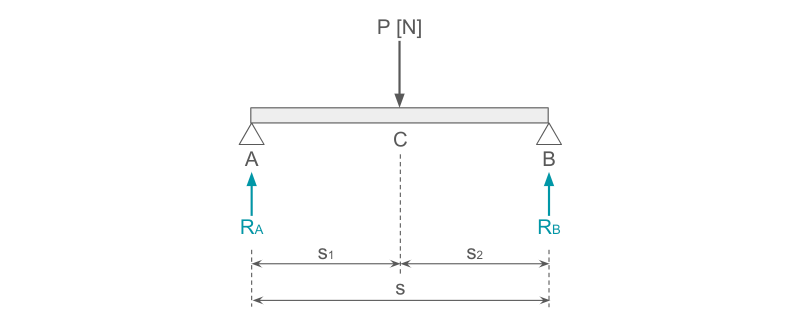
ここで、力のつり合いから、荷重Pと反力RA、RBの間には、以下の関係が成り立ちます。
P = RA + RB ・・・(1)
また、棒が回転しないためには、荷重の作用点Cにおいてモーメントが平衡になっている必要があります。
点ACの長さをs1、点CBの長さをs2とすると、以下の式が成り立ちます。
RA × s1 = RB × s2 ・・・(2)
式(1)(2)より、点A、Bに作用する反力RA、RBがそれぞれ求まります。
以上をまとめると、集中荷重が作用する梁では、①力のつり合いと②モーメントのつり合いから、支点に作用する反力が求まります。
ちなみに、これは荷重が複数作用する場合でも同じです。
点C以外の箇所に荷重がかかる場合でも、力のつり合いとモーメントのつり合いを考えることで、支点に作用する反力RA、RBを求めることができます。
分布荷重による反力の求め方
つづいては、分布荷重が作用する場合の反力の求め方です。
分布荷重の場合も、基本的には集中荷重と同じで、①力のつり合いと②モーメントのつり合いから反力が求まります。
下図のように、長さsの両端支持はりにおいて、点CDの範囲に等分布荷重w[N/m]が作用している場合を考えます。
w[N/m]は単位長さあたりの荷重です。
ここで、点CDの長さは s-s2-s1 で表されます。
したがって、はりに作用する全体の荷重は w×(s-s2-s1) [N]です。
つまり、分布荷重がはたらく点CD間の中心を点Eとすると、等分布荷重は、点Eに大きさ w(s2-s1) の集中荷重がはたらく場合とイコールで考えることができます。
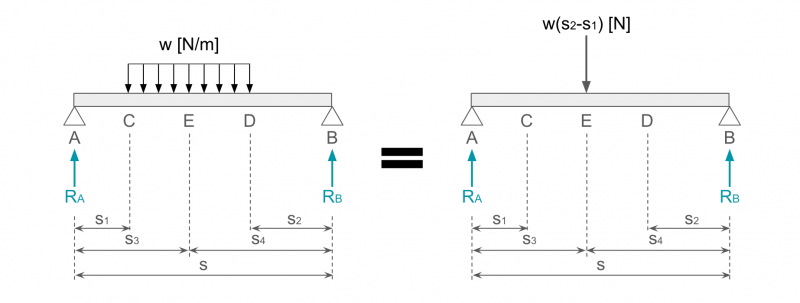
点A、Bにはたらく反力をそれぞれRA、RBとすると、①力のつり合い、および②モーメントのつり合いから、以下の式が成り立ちます。
w (s-s2-s1) = RA + RB ・・・(3)
RA × s3 = RB × s4・・・(4)
式(3)(4)より、点A、Bに作用する反力RA、RBがそれぞれ求まります。
以上をまとめると、等分布荷重が作用する梁は、集中荷重と同様に考えることができ、①力のつり合いと②モーメントのつり合いから、支点に作用する反力が求まります。
ちなみに、ここでは等分布荷重(位置に関係なく大きさが一定の荷重)について説明しましたが、位置によって荷重の大きさが変わる場合は、分布荷重w(x)を距離で積分する必要があります。
式で表すと以下のとおりです。
P = ∫w(x)dx
これを①力のつり合い、および②モーメントのつり合い式に当てはめることで、分布荷重による反力が求まります。
まとめ:梁にはたらく反力は力のつり合い・モーメントのつり合いで求められる

記事のポイントをまとめます。
- 梁とは、構造物において荷重を受け持つ部位のこと
- 水平方向にわたる部材が梁、垂直方向に立つ部材が柱
- 梁や柱の役割は、荷重の受け持ちと分散化
- 垂直方向のみ固定されるのが単純支持、垂直・水平・回転方向が固定されるのが固定支持
- 点で作用するのが集中荷重、面で作用するのが分布荷重
- 力のつり合い・モーメントのつり合いを考えることで梁にはたらく反力が求められる
以上です。
梁にはたらく荷重と反力を求められることは、機械設計エンジニアとしての基本。
「1回ではよく理解できなかった」という方は、繰り返し読んで使いこなせるようにしておきましょう。
次の記事はこちら。




コメント
分布荷重による反力の求め方で、
「ここで、点CDの長さは s2-s1 で表されます。」
という記述が理解できませんでした。
私は、点CDの長さは S-s2-s1だと思うのですが、、、。
コメントありがとうございます。
ご指摘のとおり、s-s1-s2が正しい値でしたので修正しました。
混乱させてしまいすみません。